isthas.blogg.se

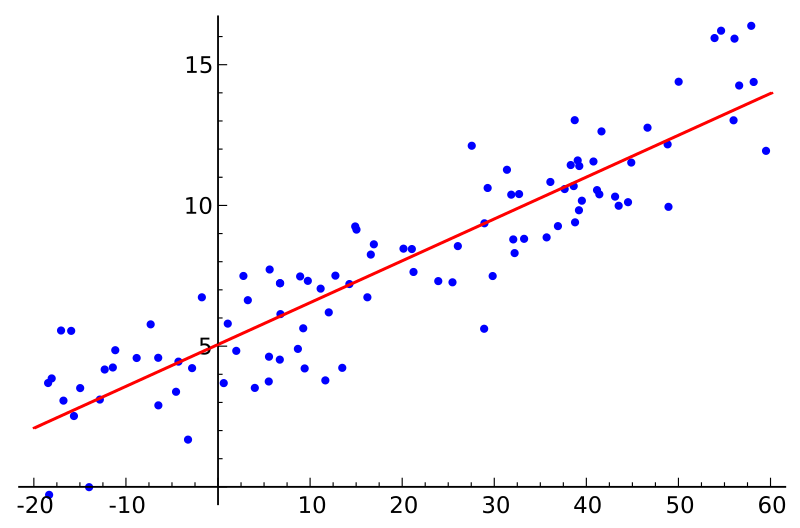
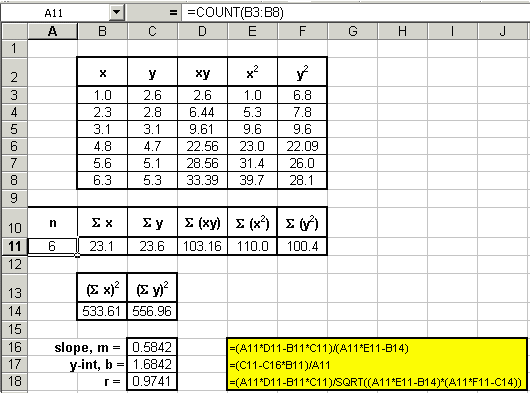
Implicitly applying regression to the sample data. (Note that the limits of the summation, which are i to n,Īnd the summation indices on x and y have been omitted.) With n data points, the slope, y-intercept and correlation coefficient, r, To the data and determine these constants. It is not necessary for us to plot the data in order to If we expect a set of data to have a linear correlation, (ValuesĬlose to 1 indicate excellent linear reliability.))Įnter your data as we did in columns B and C. The linear relationship between the x and y values. Or R, the correlation coefficient gives us a measure of the reliability of Statistical texts show the correlation coefficient as " r", butĮxcel shows the coefficient as " R". Recall that the R-squared value is the square of the correlation coefficient. Trendline and display its slope, y-intercept Let's enter the above data into an Excel spread sheet, We can then find the slope, m, and y-intercept, b,įor the data, which are shown in the figure below. Of course, this relationship is governed by the familiar equation We can plot the data and draw a "best-fit" straight line through the data. There exists a linear relationship between the variables x and y, You may also wish to take a look at how we analyzed actual The first true tells LINEST not to force the y-intercept to be zero and the second true tells LINEST to return additional regression stats besides just the slope and y-intercept.(See our Tutorial Page for more information about By the way, you might wonder what the true arguments do. I actually don’t know what the second element is.

The first element in the third row displays the correlation coefficient. From left to right, the first row displays the slope and y-intercept, the second row displays the standard error of the slope and y-intercept. The second image below shows the results of the function. This is the way to execute an array function. Instead, hold down shift and control and then press enter. Type LINEST(, use the mouse to select your y-data, type a comma, use the mouse to select your x-data, type another comma, then type true twice separated by a comma and close the parentheses. Hit the equal sign key to tell Excel you are about to enter a function. You can select up to 5 rows (10 cells) and get even more statistics, but we usually only need the first six. Since it is an array function, select 6 cells (2 columns, 3 rows). The images below and the following text summarize the mechanics of using LINEST in Excel. (As an aside, in physics we would rarely force the y-intercept to be zero in the fit even if we expect it to be zero because if the y-intercept is not zero, it may reveal a systematic error in our experiment.) Notice that the slope of the fit will be equal to 1/k and we expect the y-intercept to be zero. Therefore, s is the dependent variable and should be plotted on the y-axis. That makes F the independent value and it should be plotted on the x-axis. Let’s assume that since you control the force used, there is no error in this quantity. Because linear regression aims to minimize the total squared error in the vertical direction, it assumes that all of the error is in the y-variable. Hooke’s law states the F=-ks (let’s ignore the negative sign since it only tells us that the direction of F is opposite the direction of s). You systematically varied the force exerted on the spring (F) and measured the amount the spring stretched (s). Let’s say you did an experiment to measure the spring constant of a spring. The LINEST function performs linear regression calculations and is an array function, which means that it returns more than one value. To find these statistics, use the LINEST function instead. The equation for the fit can be displayed but the standard error of the slope and y-intercept are not give.

In Excel, you can apply a line-of-best fit to any scatterplot.